matrix类题目

1. 行、列、宫、斜线判断的，直线的思维是用 list 来存放各自的判断。顺着这个思路进一步优化：用int代替list，用位运算。
2. 涉及展开的题目，用类似 zip(*matrix)[::-1] 旋转。题目54、59
3. 涉及到坐标 i,j 的题目，可以用一个数字num代替，坐标是 divmod(num,width)

待整理

回溯/递归/dp类题目

滑动窗口类题目/字符串

待总结：

• 76 双指针+need缓存

排列/组合/放回抽样

• 排列：递归+回溯。回溯的是这次有没有被填入。
  • 题目：46/47
• 组合：用递归，f(n,k)=【取最后一个】f(n-1,k-1)+ 【不取最后一个】f(n-1,k)
  • 题目：77
• 放回抽样其实简单：

  res=[[]]
  for i in nums:
    res=[item+next_choice for item in res for next_choice in 此次可选区间]
  

双向一次遍历

有些题目可以双向一次遍历，即可得到结果，像魔法一样。

• 接水的题目
  • 1. Trapping Rain Water
  • 1. Trapping Rain Water II

756. 金字塔转换矩阵

这里注意一下，刚开始我把每种情况都回溯一下，直接超时了，加了个 if res[0]: return，只要找到一个，就不找其它的了（背的公式里面没有）

import collections

class Solution:

    def pyramidTransition(self, bottom: str, allowed: List[str]) -> bool:
        bricks=collections.defaultdict(list)

        for brick in allowed:
            bricks[brick[:2]].append(brick[2])
        res=[False]

        def pyramid_once(bottom):
            if len(bottom)==2:
                if bricks[bottom]:
                    res[0]=True
                return

            next_bottoms=['']
            for idx in range(len(bottom)-1):
                if bottom[idx:idx+2] not in bricks:
                    return

                next_bottoms=[next_bottom+i for i in bricks[bottom[idx:idx+2]]
                for next_bottom in next_bottoms
                ]


            for next_bottom in next_bottoms:
                if res[0]: return
                pyramid_once(next_bottom)


        pyramid_once(bottom)
        return res[0]

287. Find the Duplicate Number

https://leetcode.com/problems/find-the-duplicate-number/solution/
有两个思想

1. 1-n这n个数组成一个list，必然可以遍历
2. fast，slow 两个指针必然可以做到任意两个元素一一对应

658. Find K Closest Elements

https://leetcode.com/explore/learn/card/binary-search/135/template-iii/945/

使用Python的 sorted ，其time complexity 是O(log(n))

160. Intersection of Two Linked Lists

把 two pointer technique 用到极致了 https://leetcode.com/explore/learn/card/linked-list/214/two-pointer-technique/1215/discuss/49798/Concise-python-code-with-comments/156662

另一个巧妙使用 two pointer technique 的题目 (142. Linked List Cycle II)

collection

题目

https://leetcode.com/explore/learn/card/hash-table/184/comparison-with-other-data-structures/1178/discuss/82269/Short-Python-C++

来自大佬的解答

import collections

nums1 = [1, 2, 2, 1, 2]
nums2 = [2, 2, 2]

a, b = map(collections.Counter, (nums1, nums2))

list((a & b).elements())

• map函数有并行能力
• 两个collection对象用&可以做交集
• elements是一个iterable对象

top k

a = collections.Counter(nums)
sorted(a, key=lambda i: a[i],reverse=True)[:k]

Recursion

https://leetcode.com/explore/learn/card/recursion-i/255/recursion-memoization/1662

这是一个类似斐波那契的题目，自然想到用 Recursion，但还有个更好的方法，且更快（不知道为啥更快）

class Solution:
    def climbStairs(self, n: int) -> int:
        if n==1:
            return 1
        if n==2:
            return 2
        return self.climbStairs(n-1)+self.climbStairs(n-2)

    def climbStairs2(self, n: int) -> int:
     a=b=1
     for _ in range(n):
         a,b=b,a+b
     return a

链表带环问题

这是个名问题了，学的时候没做笔记，后来被问到的时候蒙了，所以还是写一写。

思路简单，一个快指针和一个慢指针。

定理1：带环的充要条件是两个指针交汇

定理2：交汇时，慢指针一定还没有走完1圈

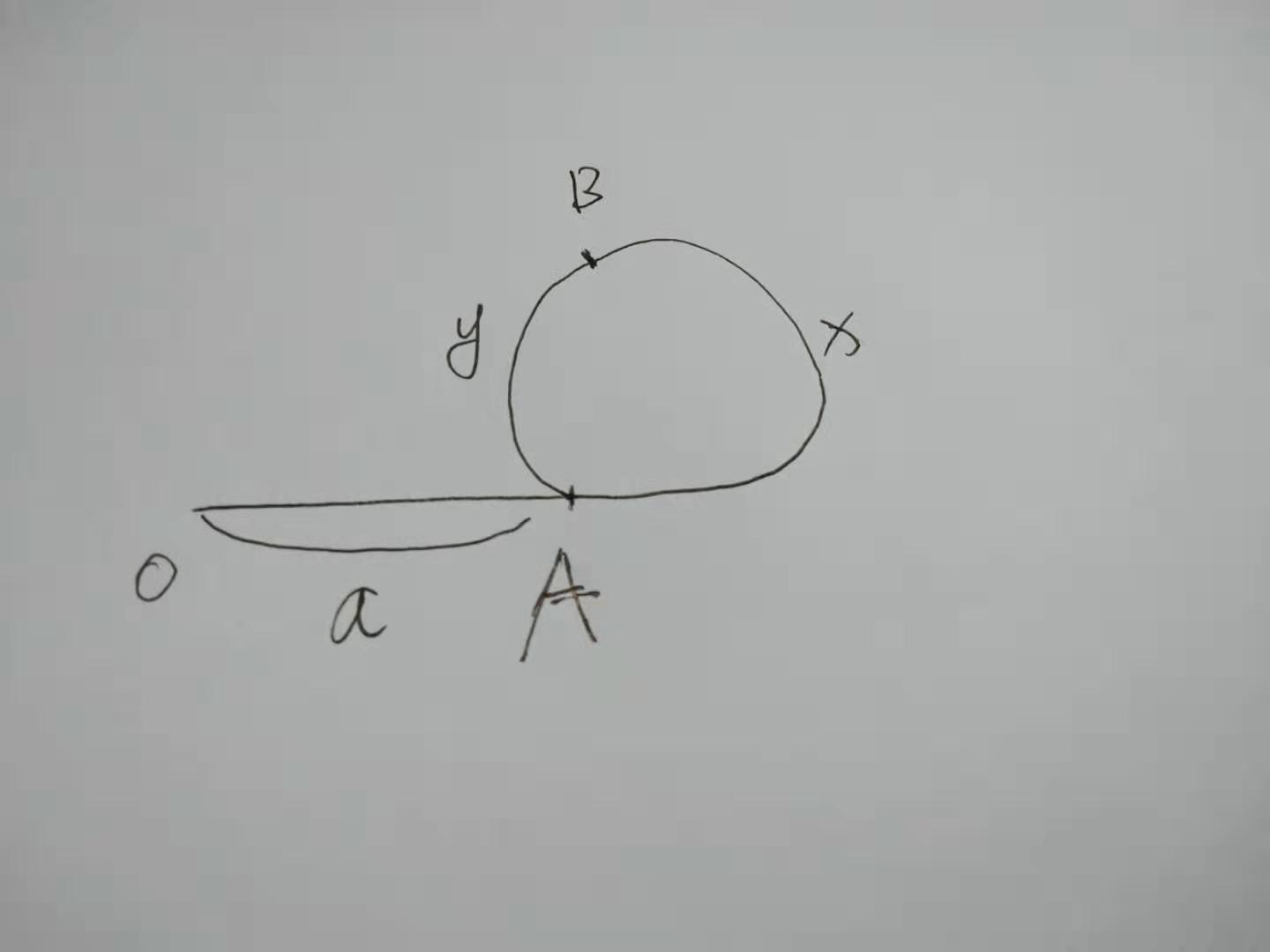
假设 快指针走2s步，慢指针走s步。相遇时快指针已经走了n圈，那么
2(a+x)=a+x+nr

a=(n-1)(x+y)+y

所以算法下一步是，在O，B各放两个慢指针，往下走，一定在A点相遇

数学类

数学类的解法一般泛用性低，但巧妙。

水库算法

有一个链表，我们不知道其长度，设计一个算法对其节点做均匀随机采样。要求最多做一次遍历。

水库算法：遍历这个链表，在遍历到第i个节点时，有 $\dfrac{1}{i}$ 的概率选择这个节点覆盖掉之前的节点选择。
(整个算法只需要遍历一次)

水库算法随机性的证明：
长度为n的链表，第i个节点被选中的充要条件是：第i个节点被选中，并且之后遍历第i+1到n个节点时，都未被替换。

这个概率就是 $\dfrac{1}{i}\times\dfrac{i}{i+1}\times\dfrac{i+1}{i+2}\times…\times\dfrac{n-1}{n}=\dfrac{1}{n}$

技巧类

最大回文

基础方法:遍历，第i到j是否是回文，遍历过程复杂度 $O(n^2)$，判断是否是回文复杂度是 O(n) ，全局复杂度 $O(n^3)$

改进1:遍历一次，每个值是回文的中心，复杂度是O(n)，判断回文的复杂度O(n)，全局复杂度是 $O(n^2)$

改进2:假设已经判断出n点左右各l距离是回文，那么右边n+l范围内是否是回文其实与左边n-l范围内的情况完全一样。那么n到n+l这个范围内的情况就不用判断了。

改进3:其实回文可以是奇数或偶数，只需要隔板插入一个字符串即可统一为一种算法。复杂度 O(n)

40亿个单词找某个单词，并且给定某个前缀，找到多少个单词的前缀是这个

其实就是 trie 树

不用1个节点对应1个字母，也可以1个节点对应一段字母。例如，in-intrest-intrested/interesting，这样。

40亿个数字找TOP1000

遍历40亿个数字，维护一个TOP1000的堆

如果允许多台机器，可以上分布式，每个 partition 求 top1000，最后合并

B+树基本知识

底层是mysql，redis是缓存；dao层操作mysql，cache层操作redis

• 如果某个sql查询比较慢，怎么办？
• 如果条件字段有索引，建立索引
• mysql底层是 B+ 树，查询复杂度 log(n)
• 如果用 hash，复杂度是 O(1)