【pytorch】基本语法
🗓 2019年12月08日 📁 文章归类: 0x26_torch
版权声明:本文作者是郭飞。转载随意,标明原文链接即可。
原文链接:https://www.guofei.site/2019/12/08/torch_operators.html
Tensor
新建
torch.empty(5, 3)
torch.ones(3, 3)
torch.ones_like(...)
torch.zeros(5, 3, dtype=torch.long)
torch.eye(5)
torch.arange(start=0, end=8, step=2) # 含头不含尾
torch.linspace(start=0, end=9, steps=5) # 均匀的取5个值,含头含尾
# 随机生成
torch.manual_seed(2) # 设置种子
print(torch.initial_seed()) 查看种子
torch.rand(5, 3)
torch.randn(5, 3)
torch.randn_like(x, dtype=torch.float)
# 从其它数据新建
torch.tensor([5.5, 3], dtype=torch.float32)
# torch.from_numpy(np.ones()) # 用上面的也可以
数据类型转换
x.int()
x.long()
x.float()
x.bool()
x.char() # int8 类型
x.double()
# 有这些类型
torch.bool
torch.int
torch.short
torch.uint8 # 这个是 ByteTensor
torch.int
torch.int8
torch.int16
torch.int32
torch.long
torch.float
torch.float16
torch.float32
torch.float64
torch.double
torch.complex32
torch.complex64
# 还有很多其它
# 四舍五入
x.round()
x.fix()
x.floor()
运算
torch.add(x, y)
# 或者
x + y
# 或者
result = torch.empty(5, 3)
torch.add(x, y, out=result)
# 大多数运算符后面可以加个下划线,表示替换运算
# 替换加
y.add_(x) # 这个会把加法的结果赋值给y
# 如 x.copy_(y), x.t_()
取数
x.size() # torch.Size([5, 3])
x.numel() # 共多少个元素
# index 和 Numpy 一样
x[:, 1]
# 获取某一行
x.select(dim=1,index=2) # 获取按照 dim 计算的 第 index 组。
# 例子的 dim=1 表示获取的是列,index=2 表示获取第 2 列
# tensor 转其它格式
x.numpy() # 转 np.array
x.tolist() # 转 list
# 转 Python 数字,只有单个元素的时候可以用
x[0][0].item()
# 注意一个特性: 共享内存
x = torch.ones(2)
y = x.numpy()
x += 1
print(x, y)
# 打印:tensor([2., 2.]) [2. 2.]
# 值得一提,反过来也是这个特性
a = np.ones(5)
b = torch.from_numpy(a)
a += 1
print(a, b)
# [2. 2.] tensor([2., 2.])
reshape
# 修正:新版本已可用
# reshape 也可以做下面这些事,但不能reshape到1维(?不知道为什么要这么设计)
x = torch.randn(4, 4)
x.reshape(2, -1)
x.reshape(-1)
GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 先生成,再放入 GPU
x = torch.randn(4, 4).to(device)
# 或者直接在 GPU 生成
x = torch.randn(4, 4, device=device)
# 也可以是字符串
# device = 'cpu' # device = 'cuda'
# ...to(device)
基本运算
x.sqrt()
x.square()
x.exp()
x.cos()
x.cosh()
x.acos()
x.acosh()
x.arccos()
x.arccosh()
矩阵运算
x = torch.rand(5, 5)
# 矩阵积
x.matmul(x)
# 矩阵的点积
x * x
U, S, V = x.svd()
eigenvalues, eigenvectors = x.eig(eigenvectors=False) # 默认不计算特征向量
x1.diag() # 对角线
矩阵变换
x.flip(dim) # 按照 dim 确定的维度翻转
x.t() # 转秩
x.tril(k=0) # 下三角矩阵
x.triu(k=0) # 上三角矩阵
# cat
x1 = torch.rand(3, 2)
x2 = torch.rand(3, 2)
torch.cat([x1, x2], dim=0)
# 分割
x = torch.arange(0,12,step=1).reshape(2,6)
x.chunk(chunks=3, dim=1) # 尽量均匀分为三份
# 分为3份,大小分别是 1,3,2
torch.split(x, split_size_or_sections=(1, 3, 2), dim=1)
# 按 dim=1 分为3份,其大小分别为 1, 3, 2
where
torch.where(x1 > 0.5, x1, x2)
torch.clip(x1, min=0.4, max=0.6)
按位运算
# dtype 必须是 int 类型,最好是 uint8
x1 = torch.tensor([1, 2, 3], dtype=torch.uint8)
x2 = torch.tensor([1, 1, 1], dtype=torch.uint8)
x1 & x2 # 按位与
x1 | x2 # 按位或
~x1 # 按位非
x1 ^ x2 # 按位异或
# 以上对应的运算符为:x1.bitwise_or(x2) 等类似的东西
x1 << 1 # 移位运算
# x1.bitwise_left_shift(1)
逻辑运算
# 0 转为 False,别的数字都转为 True
x1 = torch.tensor([-0.9, 0, True, False], dtype=torch.bool)
# >、<、==、 >=、 <= 都可以
x2 = torch.rand(size=(4,)) < 0.5
# logic and:
x1 * x2
x1 *= x2
# logic or:
x1 + x2
x1 += x2
x1.logical_and(x2)
x1.logical_or(x2)
x1.logical_xor(x2)
x1.logical_xor_(x2)
x1.logical_not()
x1.logical_not_()
统计类运算
x.mean()
x.mean(dim=1,keepdim=True)
x.max()
values, indices = x.max(dim=1, keepdim=True)
x.min()
x.mode()
values, indices = x.sort(dim=1, descending=False)
x.argmin()
x.argsort()
x1.argmax(dim=1, keepdim=True)
x.histc
x.histogram
x.std
激活函数
torch.nn中的激活函数是对象的形式,用于在__init__中定义torch.nn.functional中的激活函数是函数的形式,可以直接在forward中使用
激活函数
- ReLU
ReLU(Rectifier Linear Unit),其函数为$max(0,x)$torch.nn.ReLU - ReLU6
是 hard-sigmoid 的变种$min(max(0,x),6)$torch.nn.ReLU6 - sigmoid
$1/(1+exp(-x))$
torch.nn.Sigmoid - tanh
$\dfrac{1-e^{2x}}{1+e^{-2x}}$
torch.nn.Tanh - softsign
是符号函数的连续估计$x/(abs(x)+1)$torch.nn.Softsign - softplus
是ReLU的平滑版 $log(exp(x)+1)$torch.nn.softplus - ELU(Exponential Linear Unit)
类似于softplus# 表达式为 (exp(x)+1) if x<0 else x torch.nn.ELU
| 激励函数 | 优点 | 缺点 |
|---|---|---|
| Sigmoid | 不容易出现极端值 | 收敛速度慢 |
| ReLU | 收敛速度快 | 容易出现极端值 |
torch.nn.Softmax(dim=dim)
torch.nn.Softmax2d() # 用于图片
torch.nn.LogSoftmax() # 对 softmax 取对数,对应的损失函数是 NLLLoss
2019年5月22日更新(来自吴恩达的 DeepLearning.ai 课程):
- sigmoid: never use, except output layer
- tanh: pretty much strictly superior then sigmoid
- ReLU: if you do not know which to choose, always choose ReLU
- Leaky ReLU: you may try this $max(0.01z,z)$
About derivative(自己推导一下)
- sigmoid:$g(x)=\dfrac{1}{1+e^{-z}},g’(z)=g(z)(1-g(z))$
- tanh:$g(x)=\dfrac{e^z-e^{-z}}{e^z+e^{-z}},g’(z)=1-(g(z))^2$
- ReLU/Leaky RelU: 分段函数,注意0点的情况 does not matter
卷积相关
torch.nn.Conv2d(in_channels=1 # 灰度图
, out_channels=16, kernel_size=(5, 5), stride=(1, 1)
, padding=2) # 如果像保持输出的 size 和原来一样,需要 padding = (kernel_size-1)/2 if stride=1
nn.MaxPool2d(kernel_size=2)
建立模型
import torch
import torch.nn as nn
import torch.nn.functional as F
from collections import OrderedDict
class MyNet(nn.Module):
def __init__(self):
super(MyNet, self).__init__()
# 方法1
self.fc1 = nn.Linear(10, 10)
# 方法2
self.add_module("layer2", nn.Linear(10, 10))
# 方法3
self.layer3 = nn.Sequential(OrderedDict([
("conv1", torch.nn.Conv2d(in_channels=1, out_channels=16, kernel_size=(5, 5))),
("relu1", nn.ReLU())
]))
# 方法4
self.add_module("layer4", nn.Sequential(OrderedDict([
("conv1", torch.nn.Conv2d(in_channels=1, out_channels=16, kernel_size=(5, 5))),
("relu1", nn.ReLU())
])))
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return x
my_net = MyNet()
print(my_net)
# 结果:
# MyNet(
# (fc1): Linear(in_features=10, out_features=10, bias=True)
# (layer2): Linear(in_features=10, out_features=10, bias=True)
# (layer3): Sequential(
# (conv1): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
# (relu1): ReLU()
# )
# (layer4): Sequential(
# (conv1): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1))
# (relu1): ReLU()
# )
# )
保存和载入模型
# 存
torch.save(model.state_dict(),'./model.pkh')
# 读
model.load_state_dict(torch.load('./model.pkh'))
# GPU:模型保存时,会记录设备序号,如果系统不一致会报错
# 把 GPU1 的权重加载到 GPU0 上
troch.load('model.pkh', map_location={"cuda:1":"cuda:0"})
torch.load('model.pkh',map_location=lambda storage,loc: storage)
正则化项
l1和l2
# optimizer = torch.optim.SGD(my_net.parameters(), lr=0.001, momentum=0.9)
# 原来的上面一行代码,替换成下面的多行代码,其它部分不变
weight_p, bias_p = [], []
for name, p in my_net.named_parameters():
if 'bias' in name:
bias_p += [p]
else:
weight_p += [p]
optimizer = torch.optim.SGD([{'params': weight_p, 'weight_decay': 1e-5},
{'params': bias_p, 'weight_decay': 0}],
lr=1e-2,
momentum=0.9)
dropout
dropout 用来减轻 overfitting
# torch.nn.functional.dropout
# torch.nn.functional.dropout1d
# torch.nn.functional.dropout2d
# torch.nn.functional.dropout3d
torch.nn.functional.dropout(x, p=0.5, training=True, inplace=False)
# p是丢弃概率,1表示全部丢弃
# training=False,表示在训练阶段也不生效
# 类的形式定义:
self.dropout = nn.Dropout(config.dropout)
# config.dropout = 0.5
BN
Batch Normalization
torch.nn.BatchNorm1d # 针对 2 维或者 3 维,输入是 (N, D), 或者 (N, D, L)
torch.nn.BatchNorm2d # 针对 2 维,输入 (N, C, H, W)
torch.nn.BatchNorm3d # 针对 3 维,输入 (N, C, D, H, W)
# 其中,N 是批次数
# D是数据个数
# L是数据长度
# C是通道,H是高度,W是宽度
# D是深度
torch.nn.BatchNorm1d(num_features=5, eps=1e-5
, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)
# num_features:二维(N, D) 中的 D,BatchNorm2d 中的 C
# eps:防治0值导致数据溢出
# momentum 动态均值和动态方差所用的动量
# affine 自适应调整 gamma/beta 值,若为 False 则不用它们
# track_running_stats=True 不但追踪当期的均值和方差,还根据之前批次做调整
$y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$
BN不能紧跟着dropout,否则会抖动严重
损失函数
criterion = torch.nn.L1Loss()
- 交叉熵 $H(p,q)=-\sum p(x)\log q(x)$
criterion = nn.CrossEntropyLoss() torch.nn.CrossEntropyLoss(weight) # 加权交叉熵 - MSE $MSE(y,y’)=\dfrac{\sum (y-y’)^2}{n}$
criterion = nn.MSELoss() - 自定义。例如,预测销量时,多预测一个损失1元,少预测1个损失10元。
$Loss(y,y’)=\sum f(y_i,y_i’)$,
其中,\(f(x,y)=\left\{\begin{array}{ccc}a(x-y)&x>y\\ b(y-x)&x\leq y\end{array}\right.\) - 多标签二分类任务中的损失函数,每个预测值有 n 个 0/1
torch.nn.BCELoss torch.nn.BCEWithLogitsLoss
优化器
AUTOGRAD
# 方法1
x = torch.ones(2, 2, requires_grad=True)
# requires_grad 默认为 False
# 方法2
x = torch.ones(2, 2)
x.requires_grad = True
y = x + 2
# y.requires_grad 为 True
# y.grad_fn 非空
案例:
y = x + 2
# 只要 x.requires_grad == True,那么对 x 的大多数运算都符合:
# y.requires_grad 为 True
# y.grad_fn 非空
z = y * y * 3
k = z.mean()
# 同上,z.requires_grad 和 k.requires_grad 都是 True
x.requires_grad如果设定为 Ture,后面用到y的变量都会计算梯度y.grad_fn是与梯度计算有关的函数
# 求导数
k.backward() # 开始计算梯度
print(x.grad) # 返回梯度值
# 1. 返回 dk/dx_ij,形式是矩阵
# 2. 只会给出叶子的导数。所以 z.grad 没有值。因为计算这个值往往意义不大
# 3. 如果确实需要 z.grad,提前声明 z.retain_grad()
x.is_leaf, y.is_leaf # (True, False)
要点:
k.backward()只能运行一次k.backward(retain_graph=True)可以运行多次,但结果为上一次的累加,(会导致内存占用较多?)
开关梯度计算
x = torch.ones(2, 2, requires_grad=True)
# 方法1. 使用 with
with torch.no_grad():
y = x + 2
print(y.requires_grad) # False
# 方法2. 使用装饰器
@torch.no_grad()
def func(x):
return x + 2
y = func(x)
print(y.requires_grad) # False
# 相反的运算是 torch.enable_grad(),可以嵌入到 no_grad() 代码块里面
# 如果 x 本身没有设置 requires_grad=True,那么即使 enable_grad(),它也不生效
# 方法3. 全局打开/关闭
torch.set_grad_enabled(True)
torch.set_grad_enabled(False)
# ???
# 如果 out 是一个 tensor 数据类型的矢量,那么这样
v = torch.tensor([1.0, 2, 3])
y.backward(v)
# ???但我没搞清楚这个对应哪个数学公式


tf.train.GradientDescentOptimizer # 如果每次只传入batch,那么就变成随机梯度下降
tf.train.AdadeltaOptimizer
# 下面两个是常用的高阶Optimizer
tf.train.MomentumOptimizer # 学习率不只是考虑这一次的学习趋势,而且考虑上一次的学习趋势
tf.train.AdamOptimizer
tf.train.RMSPropOptimizer # alpha go所使用的优化器
torch中的优化器
optimizer = torch.optim.SGD(my_model.parameters(), lr=learning_rate)
optimizer = torch.optim.Adam(my_model.parameters(),weight_decay =0.0001) # weight_decay 是 L2 penalty
1. SGD类
1.1 BGD
batch gradient descent, 就是输入全部数据求得平均误差,然后以此为依据,进行一次迭代更新
$\theta=\theta-\alpha \nabla_\theta J(\theta)$
优点:
- cost fuction若为凸函数,能够保证收敛到全局最优值;若为非凸函数,能够收敛到局部最优值
缺点:
- 每轮迭代都需要在整个数据集上计算一次,速度慢
- 需要较大内存
- 批量梯度下降不允许在线更新模型,例如新增实例。
1.2 SGD
stochastic gradient descent, 每次读入一个数据进行计算。
$\theta=\theta-\alpha \nabla_\theta J(\theta,x^{(i)},y^{(i)})$
优点:
- 算法收敛速度快(在Batch Gradient Descent算法中, 每轮会计算很多相似样本的梯度, 这部分是冗余的)
- 可以在线更新
- 有几率跳出一个比较差的局部最优而收敛到一个更好的局部最优甚至是全局最优
缺点:
- 由于是随机抽取,梯度不可避免会有误差,因此需要调整学习率。
- 容易局部最优,容易陷入马鞍点
1.3 Mini-batch Gradient Descent
Mini-batch Gradient Descent, 将数据分为很多batch,每次随机抽取一个batch进行迭代运算。
$\theta=\theta-\alpha \nabla_\theta J(\theta,x^{(i:i+n)},y^{(i:i+n)})$
以上方法的共同缺点是:
- 学习率$\alpha$难以选择
- 往往陷入局部最优
2. Momentum
2.1 Momentum
模拟物理中的动量概念,优点是前期能够加速震荡,后期再局部最小值附近震荡时,能够抑制震荡,加快收敛。
$v_t=\gamma v_{t-1}+\nabla_\theta J(\theta)$
$\theta \leftarrow \theta-v_t$
特点:
- 下降初期,能够加速下降
- 下降中后期,康震荡
2.2 Nesterov Momentum法
在小球向下滚动的过程中,我们希望小球能够提前知道在哪些地方坡面会上升,这样在遇到上升坡面之前,小球就开始减速。这方法就是Nesterov Momentum,其在凸优化中有较强的理论保证收敛。并且,在实践中Nesterov Momentum也比单纯的 Momentum 的效果好:
$v_t=\gamma v_{t-1}+\nabla_\theta J(\theta-\gamma v_{t-1})$
$\theta \leftarrow \theta-v_t$
这样理解:$\theta-\gamma v_{t-1}$是小球对下一个位置的“展望”
3. AdaGrad法
自适应地为各个参数分配不同的学习率,能够控制每个维度的梯度方向。
AdaGrad 算法的一次迭代时这样的:
- 取一个batch
- 计算梯度,这一步与SGD一样 $g\leftarrow \dfrac{1}{m}\nabla_\theta \sum_i L(f(x^{(i)};\theta),y^{(i)})$
- 累积平方梯度 $r\leftarrow r+g\bigodot g$
- 计算更新$\Delta \theta \leftarrow \dfrac{\epsilon}{\delta+\sqrt r}\bigodot g$
- 应用迭代$\theta\leftarrow \theta+\Delta \theta$
用语言描述就是:梯度越小的分量(从图上看越平缓)下降越快,反之下降越慢。
 (图片来源于别人写的文章)
(图片来源于别人写的文章)
这个图里的划线部分是传统的 mini-batch ,如果用 AdaGrad 可以小勺一些震荡。
Adalelta
Adagrad法存在的问题:学习率单调递减,需要手动设置全局初始学习率。
Adadelta法用一阶方法,近似模拟二阶牛顿法,解决了以上问题
RMSProp法
与Momentum类似地方法,通过引入衰减系数,使每回合都衰减一定的比例。
适用于RNN
Adagrad会累加之前所有的梯度平方,而RMSprop仅仅是计算对应的平均值,因此可缓解Adagrad算法学习率下降较快的问题。
- 取一个batch
- 计算梯度,这一步与SGD一样 $g\leftarrow \dfrac{1}{m}\nabla_\theta \sum_i L(f(x^{(i)};\theta),y^{(i)})$
- $r\leftarrow \rho r+(1-\rho)g\bigodot g$
- 计算更新$\Delta \theta \leftarrow \dfrac{\epsilon}{\delta+\sqrt r}\bigodot g$
- 应用迭代$\theta\leftarrow \theta+\Delta \theta$
Adam
名称来源于 adaptive moment estimation. 根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
本质上是 Momentum + RMSProp
(tf的默认参数: $\alpha=0.001,\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8}$)
$g_t$ 是梯度
$m_t=\beta_1 m_{t-1}+(1-\beta_1) g_t$
$v_t=\beta_2 v_{t-1}+(1-\beta_2)g_t^2$
$\hat m_t=\dfrac{m_t}{1-\beta_1^t}$
$\hat v_t=\dfrac{v_t}{1-\beta_2^t}$
$\theta_{t+1}=\theta_t-\dfrac{\alpha}{\sqrt {\hat v_t}+\epsilon} \hat m_t$
学习率
学习率衰减
# 等间隔调整
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=7, gamma=0.1)
# 按步调整
torch.optim.lr_scheduler.MultiStepLR
# 指数衰减 lr * (gamma ** step)
torch.optim.lr_scheduler.ExponentialLR
# 余弦退火,学习率按余弦衰减
torch.optim.lr_scheduler.CosineAnnealingLR
# 指标在近几次没有变化时,调整学习率,最常用
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau \
(optimizer=optimizer
, mode='min'
, factor=0.5 # gamma
, patience=5 # 监控不再减少/增加的次数
, verbose=True # 触发规则后打印
, threshold=1e-4 # 触发规则的阈值
, threshold_mode='abs' # 触发规则的计算方法
, cooldown=0 # 触发规则后停止监控这么多次
, min_lr=0 # lr最小是这么多
, eps=1e-8
)
# 自定义 学习率衰减
torch.optim.lr_scheduler.LambdaLR
如何使用?
# 训练阶段,前面一堆代码
optimizer.step()
scheduler.step()
# 后面一堆代码
画一个学习率衰减图
optimizer = torch.optim.Adam(my_net.parameters(), lr=0.1)
# scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=20, gamma=0.5)
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.96)
lr_history = []
for i in range(100):
scheduler.step()
lr_history.append(optimizer.state_dict()['param_groups'][0]['lr'])
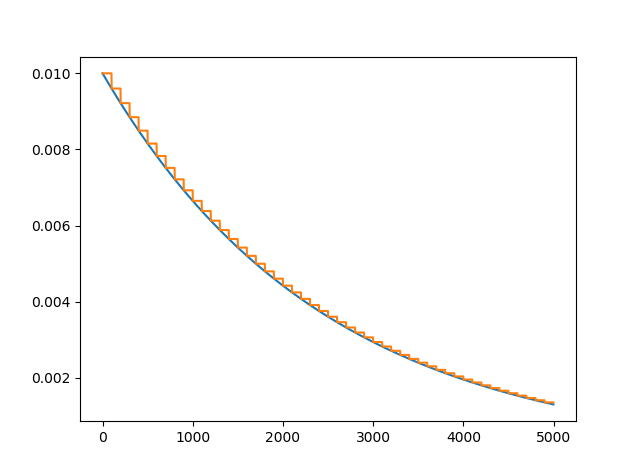
其它代码
hook
# 正向时会触发的hook
def func1(model,input,output):pass
my_net.register_forward_hook(func1)
# 反向时会触发的hook
def func2(model,grad_input,grad_output):pass
my_net.register_backward_hook(func2)
显存不够
如果模型太大,一个batch未必能放进去显存。解决:把一个 batch 分割运行,把梯度累积起来,n次后更新一次
accumulation_steps = 5 # 累积5次,然后更新一次权重
for i in range(1000):
loss = loss_func(pred, y)
loss = loss / accumulation_steps
loss.backward() # 计算 loss
if (i + 1) % accumulation_steps == 0:
optimizer.step() # 参数更新
optimizer.zero_grad() # 清空梯度
另一种情况,如果有两个独立的子任务,尽量独自前向传播
# 不要这样:
loss = loss1 + loss2
loss.backward()
# 而是这样:
loss = loss1 + loss2
loss1.backward()
loss2.backward()
关于局部最优
做梯度下降时,往往会收敛到各维度一阶导数为0的点。
我们往往觉得这是一个局部最优点,但实际上有可能是鞍点。下面是鞍点的图示:


判断鞍点的一个充分条件是:函数在一阶导数为零处(驻点)的 Hessian matrix 为不定矩阵。
这让我们想到,如果算法收敛到一个点(各维度的一阶导数一定为0),那么这个点是不定矩阵的概率是 $1-0.5^n$,n较大时,这个数接近0.
也就是说,高维空间中的鞍点数量远远大于最优点
看起来,模型几乎收敛到鞍点 (错误的结论,下面解释)
在鞍点,一个随机的扰动,就会滑出鞍点。这是 mini-batch 的优势。大部分时候收敛到的并不是鞍点
(另外,还有些鞍点是难以逃离的)
因此,高维空间里(深度学习问题上)真正可怕的不是局部最优也不是鞍点问题,而是一些特殊地形。比如大面积的平坦区域。
您的支持将鼓励我继续创作!
