基本定义

$w=f(z)$把曲线C映射到曲线$\Gamma,z_0\in C,w_0\in \Gamma,w_0=f(z_0)$
把邻域映射到邻域$z=z_0+\mid\Delta z\mid e^{i\theta},w=w_0+\mid\Delta w\mid e^{i\phi}$
如果$\lim\limits_{z\to z_0}\dfrac{\mid w-w_0 \mid}{\mid z-z_0 \mid}$存在，那么这个极限值叫做曲线C经函数$w=f(z)$映射后在$z_0$处的 伸缩率
如果$\lim\limits_{z\to z_0}(\phi-\theta)$存在，那么这个极限值叫做曲线C经函数$w=f(z)$映射后在$z_0$处的 旋转角

（保角性（conformal） 也可以这么理解：任意过$z_0$的两条曲线有一个夹角，曲线经过$f$映射后的两条曲线也有一个夹角。对于任意两条曲线，f映射前后的这两个夹角都相等。）

（TH：if $f$ is analytic and $f’(z_0)\neq 0$ then f is conformal at $z_0$）
如果$w=f(z)$在D内解析，那么$f’(z_0)=\lim\limits_{\Delta z\to 0}\dfrac{\Delta w}{\Delta z}=\lim\limits_{\Delta z\to 0}\dfrac{\mid\Delta w\mid}{\mid \Delta z\mid }e^{i(\phi-\theta)}$
$\lim\limits_{\Delta z\to 0}\dfrac{\mid\Delta w\mid}{\mid \Delta z\mid }=\mid f’(z_0)\mid$，也就是说，对于任何过$z_0$的曲线C，伸缩率都不变，这种性质叫做 伸缩率不变性
$\lim\limits_{\Delta z\to 0}(\phi-\theta)=\arg f’(z_0)$，也就是说，对于任何过$z_0$的曲线C，旋转角都不变，这种性质叫做 旋转角不变性
（$f’(z_0)\neq 0$是必要的，否则保角性将不成立）

共形映射

对于D内的映射$w=f(z)$,如果它在任一点都具有 伸缩率不变性 和 旋转角不变性 称$w=f(z)$是 第一类保角映射
如果伸缩率不变，保持角度不变但方向相反，称为 第二类保角映射
（根据上一部分的分析，如果$w=f(z)$在D内解析，那么一定在D内是保角映射）

共形映射

$w=f(z)$是区域D内的 第一类保角映射，并且当$z_1\neq z_2$，有$f(z_1)\neq f(z_2)$

Möbius transformations

Möbius transformations（分式线性映射）定义为这样的映射： $w=\dfrac{az+b}{cz+d} , (ad-bc\neq 0)$
性质（定义\(\mathbb {\hat C} =\mathbb C \cup \{ \infty \}\)）：

• 在$\mathbb{\hat C}$上是一一映射
• 是$\mathbb{\hat C \to \hat C}$的包角映射，也是唯一的满足$\mathbb{\hat C \to \hat C}$的包角映射
  （保角性很好证明，解析、非0 必保角）
• 保圆性，也就是把圆映射到圆（把直线看成无限大的圆）
• Given three distinct points $z_1, z_2, z_3 \in \mathbb{\hat C}$, there exists a unique Möbius transformation f such that $f(z_1) = 0, f(z_2) = 1, f(z_3) = \infty$.

分式线性映射可以分解成以下4种简单函数

1. $w=z+b$（b是复数），是平移映射（translation）
2. $w=ze^{i\theta},(\theta\in R)$,是旋转映射（rotation）
3. $w=rz,(r>0,r\in R)$,是相似映射（把曲线放大）（dilation）
4. $w=\dfrac{1}{z}$,是反演映射，（可以理解关于单位圆做一个对称）（inversion）

（为了形象理解反演映射，写了个动画程序,可以自行运行试试看）

# 复变函数1/z的可视化动画
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(5, 5))
ax = fig.subplots(1, 1)

line1, line2 = ax.plot(0, 0, 'bo'), ax.plot(0, 0, 'ro')

circle = np.exp(1j * 2 * np.pi * np.linspace(0, 1, 100))
line3 = ax.plot(circle.real, circle.imag)

ax.set_xlim(-1, 5)
ax.set_ylim(-1, 5)
plt.ion()  # 第一个重要的点
p = plt.show()  # 第二个重要的点

for r in np.linspace(0.2,5,200):
    z = r * np.exp(np.linspace(0, 1, 10) * 2 * np.pi * 1j)
    w = 1 / z
    plt.setp(line1, 'xdata', z.real, 'ydata', z.imag)  # 第三个重要的点
    plt.setp(line2, 'xdata', w.real, 'ydata', w.imag)  # 第三个重要的点
    plt.pause(0.1)  # 第四个重要的点

TH1 分式线性映射是共形映射

Möbius transformations 的保圆性

TH2 Möbius transformations 有保圆性。
所谓保圆性，是把圆映射到圆。（可以把直线也看成是无穷大的圆）

证明：（假设$\mid z -O \mid = r, w=f(z)$）

• 对于前三种映射，可以这样证明保角性 $w=az+b\Longrightarrow z = (w-b)/a\Longrightarrow \mid (w-b)/a -O\mid=r$
• 对于inversion，用同样的方法可以证明保圆性

直观理解如下：

# 保圆性的可视化
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(5, 5))
ax = fig.subplots(1, 1)
unit_circle = np.exp(1j * np.linspace(0, 2 * np.pi, 30))
z = 1 + 1j + unit_circle * 0.5
w = 1 / z

line1 = ax.plot(z.real, z.imag, '.r')
line2 = ax.plot(w.real, w.imag, '.b')
line3 = ax.plot(unit_circle.real, unit_circle.imag)
plt.show()

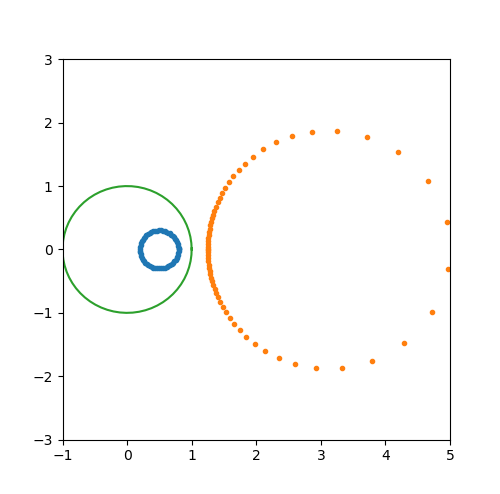
Möbius transformations 的性质3

TH3 Given three distinct points $z_1, z_2, z_3 \in \mathbb{\hat C}$, there exists a unique Möbius transformation f such that $f(z_1) = 0, f(z_2) = 1, f(z_3) = \infty$.

In fact,
$f(z)=\dfrac{z-z_1}{z-z_3}\dfrac{z_2-z_3}{z_2-z_1}$

其它性质

• TH4 The composition of two Möbius transformations is a Möbius transformation, and so is the inverse.
• TH5 Given three distinct points $z_1, z_2, z_3$ and three distinct points $w_1, w_2, w_3$, there exists a unique Möbius transformation $f : \mathbb{\hat C → \hat C}$ that maps $z_j$ to $w_j$, j = 1, 2, 3. （用TH3和TH4可证明）

The Riemann Mapping Theorem

wiki, coursera

If D is a simply connected domain (= open, connected, no holes) in the complex plane, but not the entire complex plane, then there is a conformal map ( = analytic, one-to-one, onto) of D onto the open unit disk D.

参考资料

coursera:Introduction to Complex Analysis
李红：《复变函数与积分变换》高等教育出版社
“十五”国家规划教材《复变函数与积分变换》高等教育出版社
钟玉泉：《复变函数论》高等教育出版社