OLS假设等方差，GLS可以在异方差的情况下得到无偏一致估计量。如果将等方差看成是异方差的特例，那OLS就可以看成是GLS的特例了。
普通最小二乘(OLS)，带权重的最小二乘(WLS)和广义最小二乘(GLS)，都是同一个东西 简单地说,用回归变量X来拟合响应变量Y，其中Y中的每个变量，存在内部方差(var)和外部协方差(cov),一起构成协方差阵(vcv) 因为X一般当做固定的，所以Y的协方差阵其实也就是误差项的协方差阵 1.如果存在外部协方差,即协方差阵不是对角阵，就是广义最小二乘 2.如果协方差阵是对角阵，且对角线各不相等，就是权重最小二乘 3.如果协方差阵是对角阵，且对角线相同，就是普通最小二乘 公式都是一样的 min RSS=误差项T * vcv-1 * 误差项 （T是转置, -1是逆矩阵）
理论
用于解决异方差性\(\text{diag}(\Sigma)\)
加权最小二乘法实际上是做这个最优化：$\sum w_i(y_i-f(x_i))^2$
实现
WLS knowing the true variance ratio of heteroscedasticity
step1. 导入包，造数据
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
df = pd.DataFrame()
df.loc[:, 'x'] = np.linspace(start=0, stop=20, num=60)
df.loc[:, 'w'] = [1] * 30 + [5] * 30
df.loc[:, 'const'] = 1
df.loc[:, 'y'] = 2 * df.x + df.w * np.random.randn(60) + 3
step2. 拟合
import statsmodels.api as sm
lm_s = sm.WLS(df.y, df.loc[:, ['const', 'x']], weights=1. / (df.w ** 2)).fit()
step3. 画图
from statsmodels.sandbox.regression.predstd import wls_prediction_std
prstd, iv_l, iv_u = wls_prediction_std(lm_s)
# predstd : standard error of prediction
# interval_l, interval_u : lower und upper confidence bounds
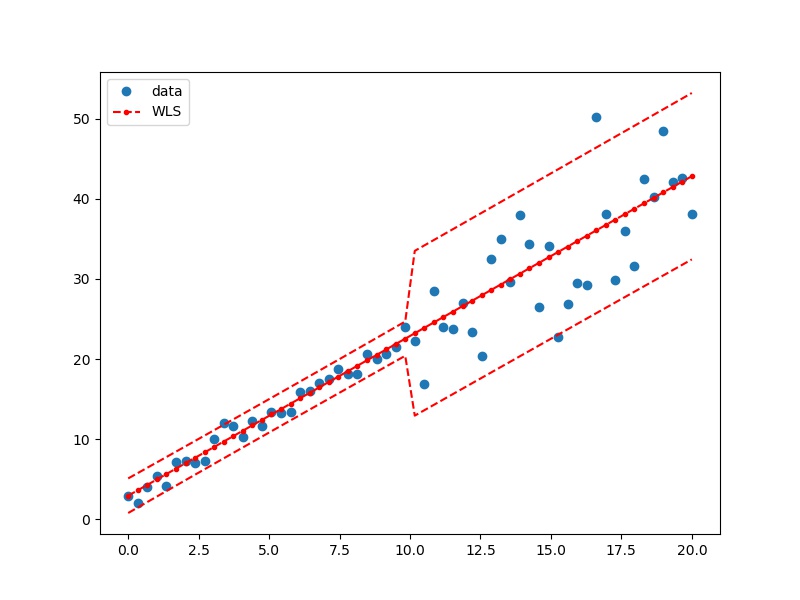
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(df.x, df.y, 'o', label="data")
ax.plot(df.x, lm_s.predict(df.loc[:, ['const', 'x']]), 'r--.', label="WLS")
ax.plot(df.x, np.array([iv_l,iv_u]).T, 'r--', label="bounds")
ax.legend(loc='best')
plt.show()
