优化器

官网解释1
官网解释2

tf.train.GradientDescentOptimizer # 如果每次只传入batch，那么就变成随机梯度下降
tf.train.AdadeltaOptimizer

# 下面两个是常用的高阶Optimizer
tf.train.MomentumOptimizer # 学习率不只是考虑这一次的学习趋势，而且考虑上一次的学习趋势
tf.train.AdamOptimizer

tf.train.RMSPropOptimizer # alpha go所使用的优化器

优化器详解

1. SGD类

1.1 BGD

batch gradient descent, 就是输入全部数据求得平均误差，然后以此为依据，进行一次迭代更新

$\theta=\theta-\alpha \nabla_\theta J(\theta)$

优点:

• cost fuction若为凸函数，能够保证收敛到全局最优值；若为非凸函数，能够收敛到局部最优值

缺点:

• 每轮迭代都需要在整个数据集上计算一次，速度慢
• 需要较大内存
• 批量梯度下降不允许在线更新模型，例如新增实例。

1.2 SGD

stochastic gradient descent, 每次读入一个数据进行计算。

$\theta=\theta-\alpha \nabla_\theta J(\theta,x^{(i)},y^{(i)})$

优点:

• 算法收敛速度快(在Batch Gradient Descent算法中, 每轮会计算很多相似样本的梯度, 这部分是冗余的)
• 可以在线更新
• 有几率跳出一个比较差的局部最优而收敛到一个更好的局部最优甚至是全局最优

缺点：

1. 由于是随机抽取，梯度不可避免会有误差，因此需要调整学习率。
2. 容易局部最优，容易陷入马鞍点

1.3 Mini-batch Gradient Descent

Mini-batch Gradient Descent, 将数据分为很多batch，每次随机抽取一个batch进行迭代运算。

$\theta=\theta-\alpha \nabla_\theta J(\theta,x^{(i:i+n)},y^{(i:i+n)})$

以上方法的共同缺点是：

1. 学习率$\alpha$难以选择
2. 往往陷入局部最优

2. Momentum

2.1 Momentum

模拟物理中的动量概念，优点是前期能够加速震荡，后期再局部最小值附近震荡时，能够抑制震荡，加快收敛。

$v_t=\gamma v_{t-1}+\nabla_\theta J(\theta)$
$\theta \leftarrow \theta-v_t$
特点：

• 下降初期，能够加速下降
• 下降中后期，康震荡

2.2 Nesterov Momentum法

在小球向下滚动的过程中，我们希望小球能够提前知道在哪些地方坡面会上升，这样在遇到上升坡面之前，小球就开始减速。这方法就是Nesterov Momentum，其在凸优化中有较强的理论保证收敛。并且，在实践中Nesterov Momentum也比单纯的 Momentum 的效果好：

$v_t=\gamma v_{t-1}+\nabla_\theta J(\theta-\gamma v_{t-1})$
$\theta \leftarrow \theta-v_t$

这样理解：$\theta-\gamma v_{t-1}$是小球对下一个位置的“展望”

3. AdaGrad法

自适应地为各个参数分配不同的学习率，能够控制每个维度的梯度方向。

AdaGrad 算法的一次迭代时这样的：

• 取一个batch
• 计算梯度，这一步与SGD一样 $g\leftarrow \dfrac{1}{m}\nabla_\theta \sum_i L(f(x^{(i)};\theta),y^{(i)})$
• 累积平方梯度 $r\leftarrow r+g\bigodot g$
• 计算更新$\Delta \theta \leftarrow \dfrac{\epsilon}{\delta+\sqrt r}\bigodot g$
• 应用迭代$\theta\leftarrow \theta+\Delta \theta$

用语言描述就是：梯度越小的分量（从图上看越平缓）下降越快，反之下降越慢。

（图片来源于别人写的文章）

这个图里的划线部分是传统的 mini-batch ，如果用 AdaGrad 可以小勺一些震荡。

Adalelta

Adagrad法存在的问题：学习率单调递减，需要手动设置全局初始学习率。
Adadelta法用一阶方法，近似模拟二阶牛顿法，解决了以上问题

RMSProp法

与Momentum类似地方法，通过引入衰减系数，使每回合都衰减一定的比例。
适用于RNN
Adagrad会累加之前所有的梯度平方，而RMSprop仅仅是计算对应的平均值，因此可缓解Adagrad算法学习率下降较快的问题。

• 取一个batch
• 计算梯度，这一步与SGD一样 $g\leftarrow \dfrac{1}{m}\nabla_\theta \sum_i L(f(x^{(i)};\theta),y^{(i)})$
• $r\leftarrow \rho r+(1-\rho)g\bigodot g$
• 计算更新$\Delta \theta \leftarrow \dfrac{\epsilon}{\delta+\sqrt r}\bigodot g$
• 应用迭代$\theta\leftarrow \theta+\Delta \theta$

Adam

名称来源于 adaptive moment estimation. 根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。
本质上是 Momentum + RMSProp

（tf的默认参数: $\alpha=0.001,\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8}$）
$g_t$ 是梯度
$m_t=\beta_1 m_{t-1}+(1-\beta_1) g_t$
$v_t=\beta_2 v_{t-1}+(1-\beta_2)g_t^2$
$\hat m_t=\dfrac{m_t}{1-\beta_1^t}$
$\hat v_t=\dfrac{v_t}{1-\beta_2^t}$
$\theta_{t+1}=\theta_t-\dfrac{\alpha}{\sqrt {\hat v_t}+\epsilon} \hat m_t$

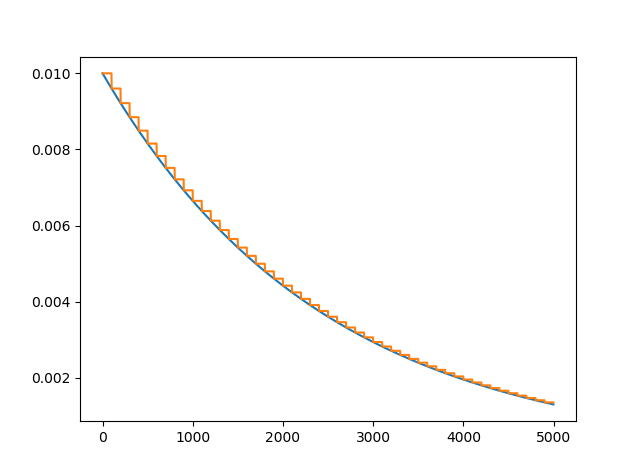
学习率

tf.train.exponential_decay 指数下降法减小学习率
decayed_learning_rate=learning_rate * decay_rate ** (global_step/decay_steps)

learning_rate=tf.train.exponential_decay(0.01,global_step=10000,decay_steps=100,decay_rate=0.96,staircase=True)

staircase=True时，(global_step/decay_steps)会转化成整数，使得学习率阶梯下降

学习率的图：

import tensorflow as tf
sess=tf.Session()

global_step_=tf.constant(0)
c=tf.train.exponential_decay(learning_rate=0.01,global_step=global_step_,decay_steps=100,decay_rate=0.96,staircase=False)
d=tf.train.exponential_decay(learning_rate=0.01,global_step=global_step_,decay_steps=100,decay_rate=0.96,staircase=True)
steps,learning_rates_c,learning_rates_d=[],[],[]
for i in range(1000):
    steps.append(i)
    learning_rates_c.append(sess.run(c,feed_dict={global_step_:i}))
    learning_rates_d.append(sess.run(d,feed_dict={global_step_:i}))


import matplotlib.pyplot as plt
plt.plot(steps,learning_rates_c)
plt.plot(steps,learning_rates_d)
plt.show()

用法案例

import tensorflow as tf
TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True)

x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 10 == 0:
            LEARNING_RATE_value = sess.run(LEARNING_RATE)
            x_value = sess.run(x)
            print ("After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value))

关于局部最优

做梯度下降时，往往会收敛到各维度一阶导数为0的点。
我们往往觉得这是一个局部最优点，但实际上有可能是鞍点。下面是鞍点的图示：

判断鞍点的一个充分条件是：函数在一阶导数为零处（驻点）的 Hessian matrix 为不定矩阵。

这让我们想到，如果算法收敛到一个点（各维度的一阶导数一定为0），那么这个点是不定矩阵的概率是 $1-0.5^n$，n较大时，这个数接近0.
也就是说，高维空间中的鞍点数量远远大于最优点
看起来，模型几乎收敛到鞍点 （错误的结论，下面解释）

在鞍点，一个随机的扰动，就会滑出鞍点。这是 mini-batch 的优势。大部分时候收敛到的并不是鞍点
（另外，还有些鞍点是难以逃离的）

因此，高维空间里（深度学习问题上）真正可怕的不是局部最优也不是鞍点问题，而是一些特殊地形。比如大面积的平坦区域。

参考文献

TF官网-tf.nn