多目标最优化通常记为 MOP(multiobjective programming)
是研究多于一个的目标函数在给定区域上的最优化
定义
$\min\limits_{x\in D} (f_1(x), f_2(x),…, f_p(x))$
$x_0\in D$，如果$\exists x’ \in D$，使得$f_k(x’)<f_k(x_0), k=1,2,…,p$，称$x_0$为 劣解
$x_0\in D$，如果不存在$x’ \in D$，使得$f_k(x’) \leq f_k(x_0), k=1,2,…,p$，称$x_0$为 有效解
$x_0\in D$，如果不存在$x’ \in D$，使得$f_k(x’) < f_k(x_0), k=1,2,…,p$，称$x_0$为 弱有效解
解法1：权重法
按照每一项的重要程度，赋予权重
$\min\limits_{x\in D} \sum\limits_{i=1}^p \lambda_i f_i(x)$
解法2：分层排序法
将目标函数按其重要程度排成一个次序，然后分别在前一个目标函数的最优解集中，求出后一个目标函数的最优解集。如此便可以转化成p个单目标最优化问题。
解法2的变种
不是求前一个目标函数的最优解集，而是允许一定偏差的集合
stable matching
这是一个讲座中听到的模型，首先定义一下可行解和有效边界。
- attainable region
- 可行解，约束条件所定义的集合，这里我们期望集合是凸的
- efficient frontier
- 可行解集合的边界
一个容易理解的事实：如果去掉约束条件后求得的最优点不在可行解内，
那么加权法或分层排序法所得到的解一定在efficient frontier上。并且加权法不同的权重对应efficient frontier上不同的点。
工业界具体应用时往往对权重存在争议，也就是对efficient frontier 上哪个点作为最优解存在争议。
算法1
找一个 Utopai Point ，定义 efficient frontier 上，距离 Utopai Point 最近的点作为最优点（起名为 compromise solution）。
（其中，距离可以使用$l_p$距离）
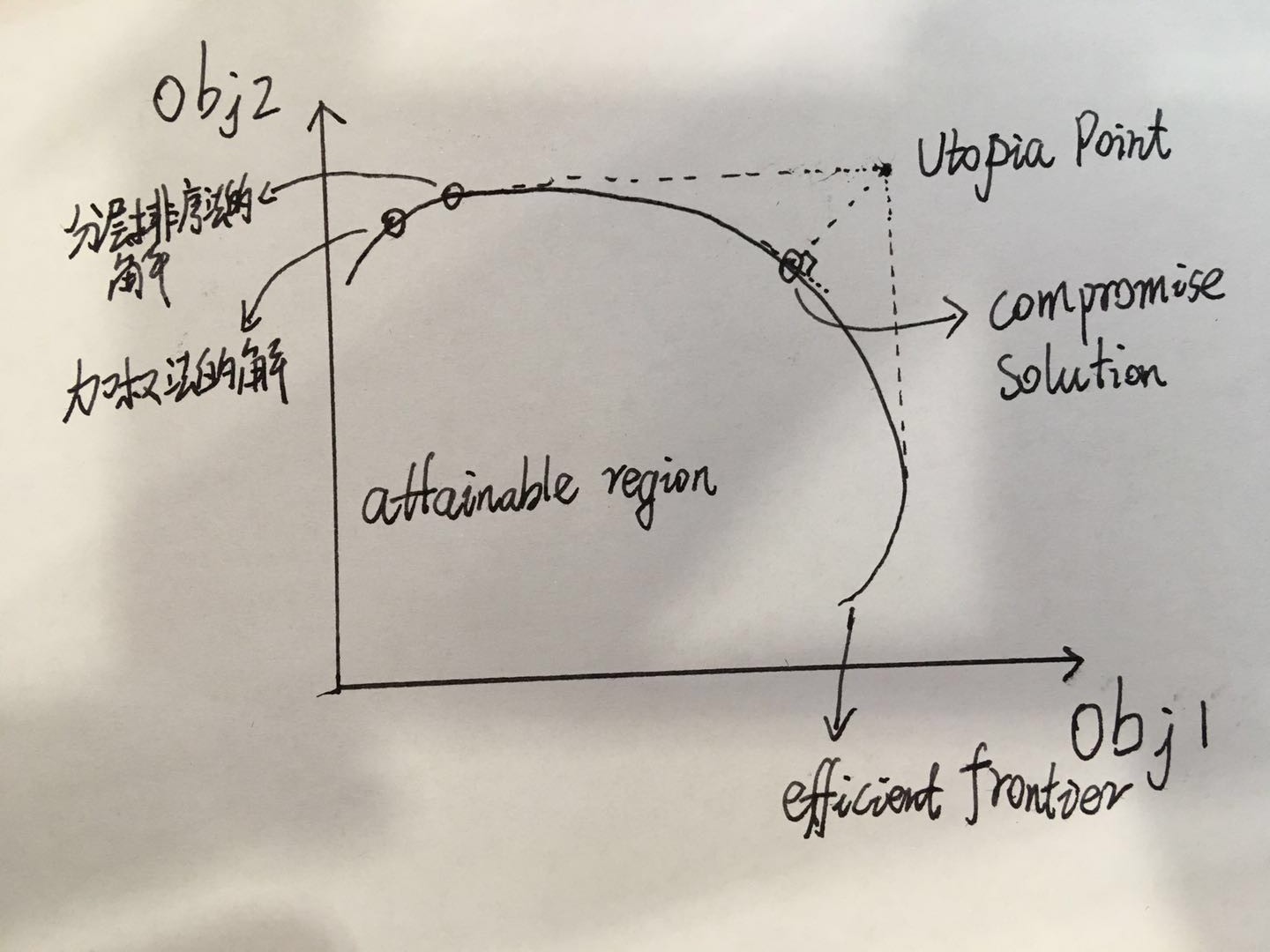
模型1的示意图
Utopai Point 有两种计算方案
各个最大法
在约束下，分别求$\max f_i$
得到$(f_1^* , f_2^* ,f_3^* ,…, f_n^* )$，这个点作为Utopai Point
业务法
从业务逻辑出发，给出每一个指标$f_i$的最理想的值。
得到$(f_1^* , f_2^* ,f_3^* ,…, f_n^* )$，这个点作为Utopai Point
算法2
此模型可以应用于动态过程，s为期数，当前为第t期，已知过去t-1期的情况。
$D_k(s)=U_k-f_k(x(s)), \forall k,s$
其中，k是指第k个方程，s指第s期
$U_k$是 Utopai Point，$f_k$是第k个目标
$w_k(t)=\dfrac{1}{t-1}\sum\limits_{s=1}^{t-1}D_k(s)$
$w_k^+(t)=\max(0,w_k(t))$
目标函数是$max \sum\limits_{k=1}^K w_k^+(t) f_k(x(t))$
直观理解这种算法，就是某一项接近理想目标时，其权重变小。
参考资料
施光燕：《最优化方法》，高等教育出版社
龚纯：《Matlab最优化计算》，电子工业出版社
David R. Anderson ：《数据、模型与决策–管理科学篇》，机械工业出版社
