算法打包
已经把算法打包了，scikit-opt
def func(x):
x1, x2 = x
return 1 / x1 ** 2 + x1 ** 2 + 1 / x2 ** 2 + x2 ** 2
from sko.ASFA import ASFA
asfa = ASFA(func, n_dim=2, size_pop=50, max_iter=300,
max_try_num=100, step=0.5, visual=0.3,
q=0.98, delta=0.5)
best_x, best_y = asfa.fit()
print(best_x, best_y)
算法介绍
人工鱼群算法（artificial fish swarm algorithm）是李晓磊等人于2002年提出的一类基于动物行为的群体智能优化算法。
算子介绍
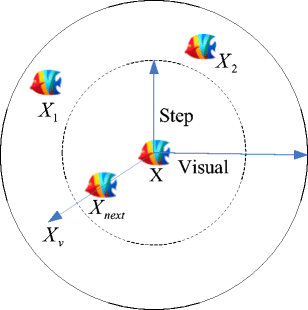
变量定义，
目标函数func(X)
人工鱼总数N
人工鱼i的位置$X_i=(x_1,x_2,…,x_n)$
鱼的每一步的最大位移 Step
最大尝试次数 $Try_{num}$
鱼的最大感知范围 visual
拥挤度阈值 delta
1. 觅食行为prey()
觅食分为两步，
第一步在感知范围内随机选取一个点
第二步判断这个随机选择的点是否比当前点更优，如果更优则向此点移动一步，否则再次尝试。
数学表示：
第一步
$X_j=X_i+visual*rand()$
（其中$X_i$是鱼当前所在的点，$X_j$是鱼感知到的点）
第二步
如果$func(X_j)$优于$func(x_i)$,那么从$X_i$向$X_j$移动一步：
$X_i^{t+1}=X_i^t+\dfrac{X_j-X_i^t}{\mid\mid X_j-X_i^t\mid\mid}\times Step\times rand()$
如果不优，回到第一步，直到尝试$Try_{num}$次,如果还是中心不更优，则进入随机行为 move()
2. 聚群行为swarm()
聚群行为会遵守两条原则：
- 尽量向伙伴移动
- 避免过分拥挤
数学表示：
计算visual范围内其他鱼的数目$n_f$和中心位置$X_c$
如果$\dfrac{func(X_c)}{n_f}>delta \times Y_i$,向中心移动一步:
$X_i^{t+1}=X_i^{t+1}+\dfrac{X_c-X_i^t}{\mid\mid X_c-X_t\mid\mid}\times step \times rand()$
如果不优，则开始觅食行为 prey()
3. 追尾行为follow()
与聚群行为的区别是，追随浓度最高的伙伴的点，而不是视野内的中心点。
数学表示：
计算visual范围内其他鱼的数目$n_f$和最优func对应的$X_j$
如果$\dfrac{func(X_j)}{n_f}>delta \times Y_i$,向这条鱼移动一步:
$X_i^{t+1}=X_i^{t+1}+\dfrac{X_j-X_i^t}{\mid\mid X_j-X_t\mid\mid}\times step \times rand()$
如果不优，则开始觅食行为 prey()
4. 随机行为move()
$X_i^{t+1}=X_i^{t}+visual \times rand()$
算法过程
算法过程比较简单，每次迭代反复调用 swarm(),follow()即可。
swarm,follow中有转向prey()的判断。prey感知几次不成功后，转入move()。所以每个算子都用到了
算法过程：
- swarm()
- follow()
- 返回1继续计算，直到达成算法结束的条件。
