算法打包
已经把算法打包了，scikit-opt
from sko.IA import IA_TSP_g as IA_TSP
ia_tsp = IA_TSP(func=cal_total_distance, n_dim=num_points, pop=500, max_iter=2000, Pm=0.2,
T=0.7, alpha=0.95)
best_points, best_distance = ia_tsp.fit()
print('best routine:', best_points, 'best_distance:', best_distance)
算法介绍
免疫算法（immune algorithm）与遗传算法很像，算法结构大致相同，都是
初始种群产生→→评价标准计算→→种群间个体信息交换→→新总群产生 这一循环过程，本质上都具有并行性。
主要区别：
- 对个体评价。遗传算法是计算个体适应度，选择父代个体的唯一标准是父代的个体适应度。免疫算法对个体的评价和选择都以 亲和度(affinity) 为标准，个体亲和度包括 抗体-抗原亲和度(匹配程度),抗体抗体亲和度（相似程度）
- 同样有交叉、变异等算子，增加了克隆选择、免疫记忆、疫苗接种等激励。
算法步骤
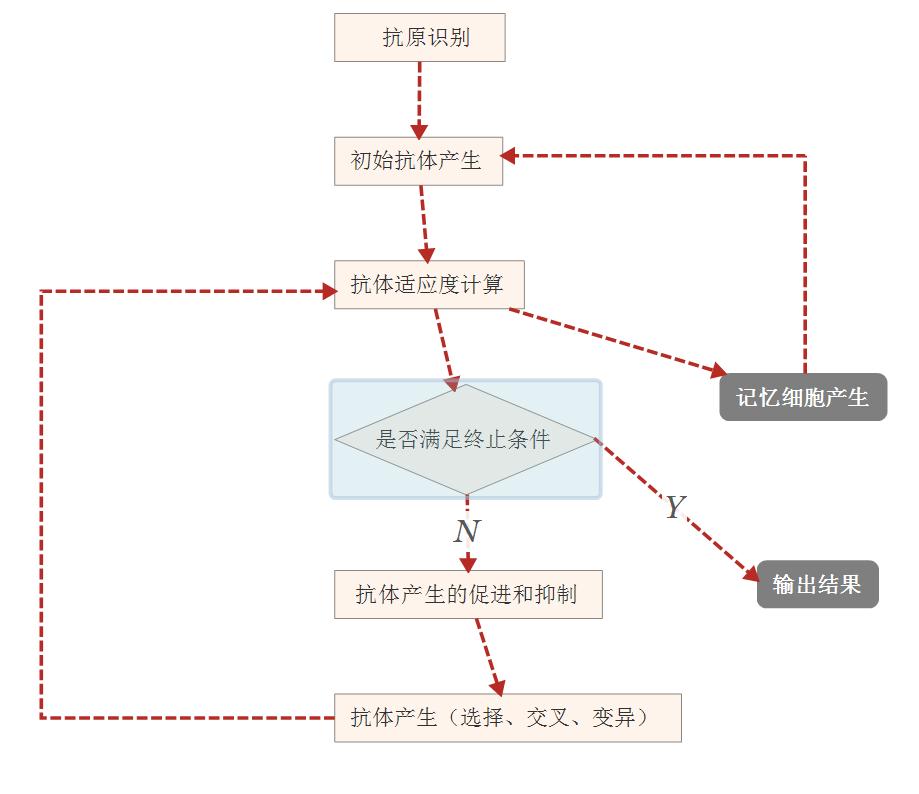
- 产生初始抗体群，随机产生N个个体，并提取全部m个记忆抗体，作为初始群体
- 对抗体进行评价，计算个体期望繁殖率P
- 形成父代群体。将初始群体按照P排序，取前N个个体作为父代群体，前m个作为记忆
- 如果满足结束条件则输出结果并退出算法
- 对N个父代群体进行选择、交叉、变异，并提取记忆细胞，构成新的群体
- 回到2
个体期望繁殖概率
1. 抗体-抗原亲和度
$A_v=\dfrac{1}{F}$
其中，F是个体v对应的目标函数值（目标是求出$\min F$）
也就是说，$A_v$越大，越希望保留
2. 抗体之间的亲和力
$S_{v,s}=\dfrac{k_{v,s}}{L}$
其中，$k_{v,s}$是两个个体v，s 相同位的个数，L是抗体长度
（其实就是杰卡德相似系数）
3. 抗体浓度
这里用伪代码表示抗体浓度的算法，
按照（2）中的亲和力公式，计算出个体v与其它所有抗体的亲和力，放入列表S
C_v=[1 for i in S if S>T].sum()/N
T是一个预先设定的阈值
4. 期望繁殖率
$P=a\dfrac{A_v}{\sum A_v}+(1-a)\dfrac{C_v}{\sum C_v}$
