算法打包
已经把算法打包了，scikit-opt
def demo_func(x):
x1, x2, x3 = x
return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2
from sko.SA import SA
sa = SA(func=demo_func, x0=[1, 1, 1])
x_star, y_star = sa.fit()
print(x_star, y_star)
算法介绍
模拟退火算法（Simulated Annealing，简称SA）的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法，其物理退火过程由以下三部分组成：
- 加温过程。其目的是增强粒子的热运动，使其偏离平衡位置。当温度足够高时，固体将熔为液体，从而消除系统原先存在的非均匀状态。
- 等温过程。对于与周围环境交换热量而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行的，当自由能达到最小时，系统达到平衡状态。
- 冷却过程。使粒子热运动减弱，系统能量下降，得到晶体结构。
- 加温过程对算法设定初温，等温过程对应算法的 Metropolis抽样过程 ，冷却过程对应 控制参数的下降。这里能量的变化就是目标函数，我们要得到的最优解就是能量最低态。其中Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以一定的概率接受恶化解，这样就使算法跳离局部最优的陷阱
特点：
- 与遗传算法、粒子群优化算法和蚁群算法等不同，模拟退火算法不属于群优化算法，不需要初始化种群操作。
- 收敛速度较慢。
- 温度管理、退火速度等对寻优结果均有影响。
算法步骤
- 初始化：取初始温度T0足够大，令T = T0，任取初始解S1。
- 对当前温度T，重复第（3）～（6）步。
- 对当前解S1随机扰动产生一个新解S2。
- 计算S2的增量df = f(S2) - f(S1)，其中f(S1)为S1的代价函数。
- 若df < 0，则接受S2作为新的当前解，即S1 = S2；否则计算S2的接受概率exp(-df/T)， 即随机产生(0,1)区间上均 匀分布的随机数rand，若exp(-df/T) > rand，也接受S2作为新的当前解S1 = S2，否则保留当前解S1。
- 如果满足终止条件Stop，则输出当前解S1为最优解，结束程序，终止条件Stop通常取为在连续若干个Metropolis链中新解S2都没有被接受时终止算法或者是设定结束温度；否则按衰减函数衰减T后返回第（2）步。
算法变种
step3：不同的随机扰动产生方法
step5：不同的概率表示形式
step6：不同的时间衰减方法
模拟退火解决TSP问题
随机扰动产生方法类似GA用于TSP问题中的mutation算子。
其余类似
直接上图
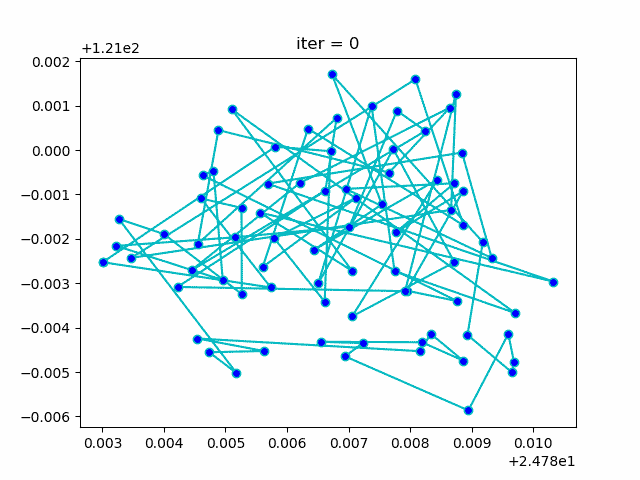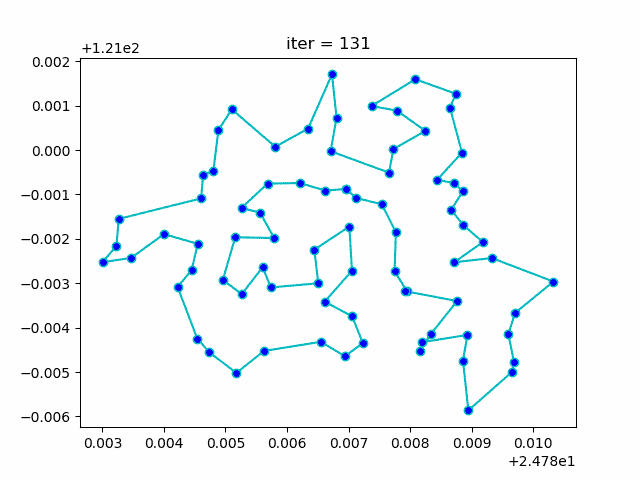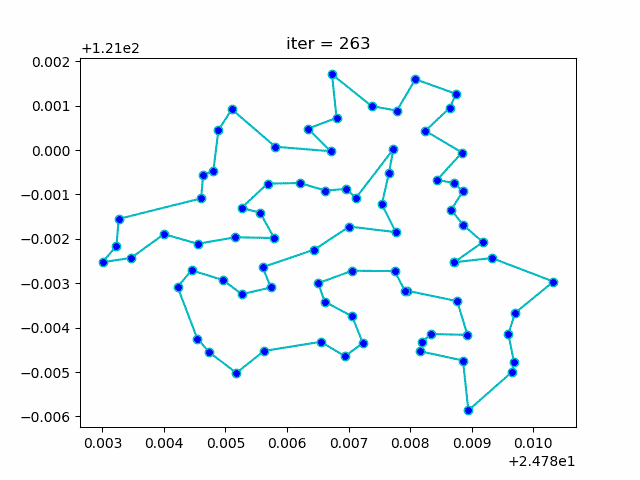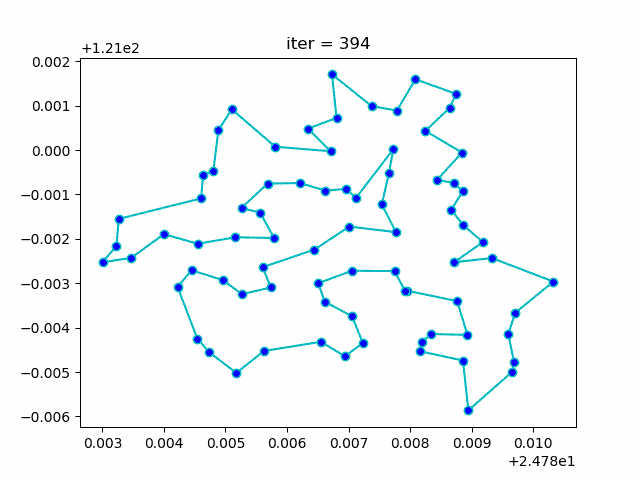
代码在 这里
