算法打包
已经把算法打包了，scikit-opt
def demo_func(x):
x1, x2, x3 = x
return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2
from sko.PSO import PSO
pso = PSO(func=demo_func, dim=3)
fitness = pso.fit()
print('best_x is ',pso.gbest_x)
print('best_y is ',pso.gbest_y)
pso.plot_history()
Matlab代码见于 【随笔】 《谁动了我的奶酪》中的粒子群算法.
粒子群优化（PSO, particle swarm optimization）算法是一种群体智能的优化算法，该算法最早由Kennedy和Eberhart在1995年提出的，该算法源自对鸟类捕食问题的研究。
算法步骤
step1:初始化位置x，速度v
step2:计算个体极值pbest， 全局极值gbest
step3:更新位置x，速度v
step4:更新权重w（可以是恒定权重或递减权重）
step5:计算个体极值pbest， 全局极值gbest
step6:如果不满足收敛条件，回到step3，继续迭代。
变量定义
问题的维度：n
第i个粒子的位置$x(i,:)=(xi1,xi2,…,xin)$
第i个粒子的速度$v(i,:)=(vi1,vi2,…vin)$
第i个粒子的历史最优$pbest(i,:)=(pi1,pi2,…pin)$
全局最优$gbest=(g1,g2,…gn)$
其它变量
r 粒子群算法的种子数量
m 粒子群算法的群体大小
max_d 最大迭代次数
r1,r2 加速权重 取[0,1]之间的随机数（每次迭代都重新生成）
c1,c2 加速常数 取2左右的数
w 惯性权重
$vmax=k*xmax (0.1<=k<=1) $
迭代算法
更新速度：\(v(i,:)=w * v(i,:)+c1 * r1 * (pbest(i,:)-x(i,:))+c2 * r2 * (gbest-x(i,:))\)
更新位置：\(x(i,:)=x(i,:)+v(i,:)\)
where,
第一部分称为“惯性”或“动量” inertia,momentum
第二部分称为“认知” cognition ，反映粒子的memory或rememberance
第三部分成为social，反映粒子群体历史经验
PSO的改进
有两种：
- 自适应变异
- 惯性权重
自适应变异
做法1：
为了解决粒子群算法容易早熟收敛，后期迭代效率不高的问题。
每次迭代后，按照一定概率重新初始化某些粒子。
做法2：
每次迭代都从全部点集中随机选取一些点，组成集合，以这些点计算全局最优gbest
权重改进
权重较大，搜索范围更广泛。
权重较小，搜索范围更精细。
方法1：随机权重法
$u=u_{min}+(u_{max}-u_{min}) * rand(0,1)$
$w=N(u,\sigma^2)$
方法2：线性递减权重
这个方法使得惯性权重越来越低，粒子的跳动能力越来越低，算法迭代到后面，稳定性越来越高
$w=w_{max}-\dfrac{t * (w_{max}-w_{min})}{t_{max}}$
其中，t是此次的迭代次数
PSO改进：速度限制
设定速度分量的最大值、最小值$v_{max},v_{min}$
认知
对于有约束
把超出约束的值设定到约束边界上
几个附件
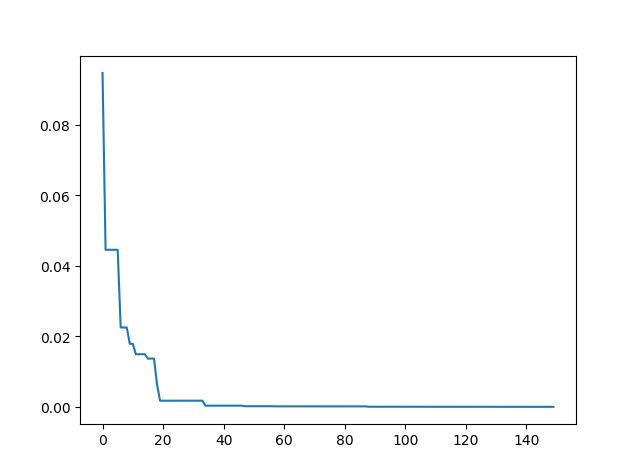
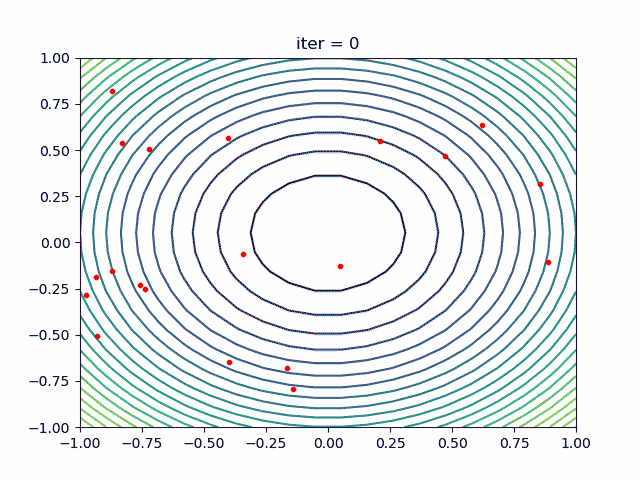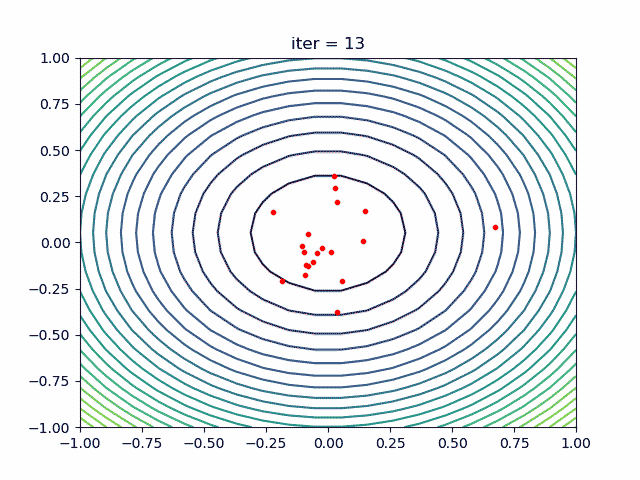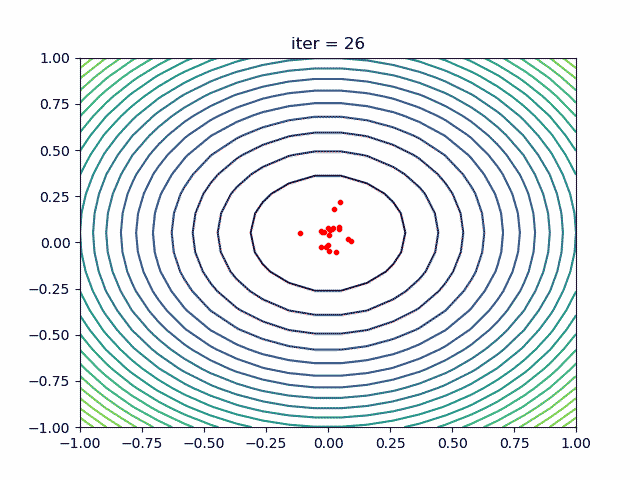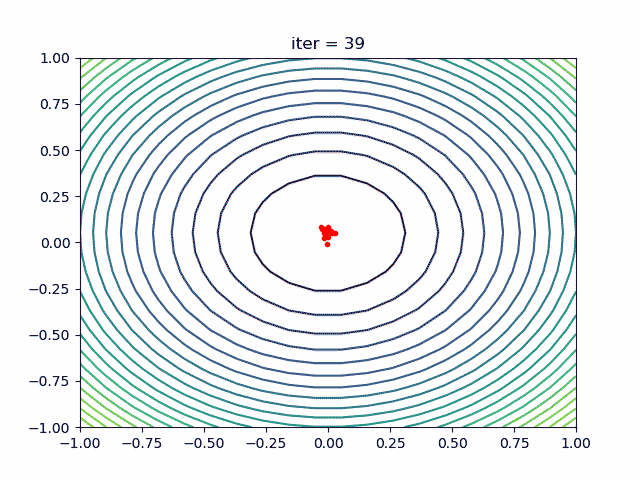
代码在 这里
