虚拟变量回归，又叫做哑变量回归（Dummy Variable Regression Models）
虚拟变量
又叫做哑变量，Dummy Variable
指的是取值0或1的变量，用来代表类别
一个分类量有k个类别时，需要引入k-1个虚拟变量
例如：
要研究大学生学习成绩和收入之间的关系，考虑到4个年级的情况未必相同，因此把年级也放到Dependent Variables里面，对年级这样构造：
$Y=a_0+a_1D_1+a_2D_2+a_3D_3+a_4X+\epsilon$
其中，$D_1$=1是大一，否则为0.
$D_2$代表大二，否则为0.
$D_3$代表大三，否则为0.
注意1
为什么表示多个类时，要用多个0-1变量，而不用一个0,1,2,3变量？
答：
如果用0,1,2,3 那么就只能以连续变量理解这个变量，认为这个变量既有大小又有刻度
注意2
为什么一个分类量有k个类别时，引入k-1个Dummy Variables， 而不是k个？
答：
如果引入k个Dummy Variables, 将会有完全的多重共线性
$D_1+D_2+D_3+D_4 \equiv 1$
加法模型
$Y=a_1+a_2D_1+a_3D_2+bX+u$
模型解释
例如，Y代表啤酒销售量，X代表收入。
$D_1=1$代表夏季，0代表冬季
$D_2=1$代表城市，0代表农村
模型是这样的：
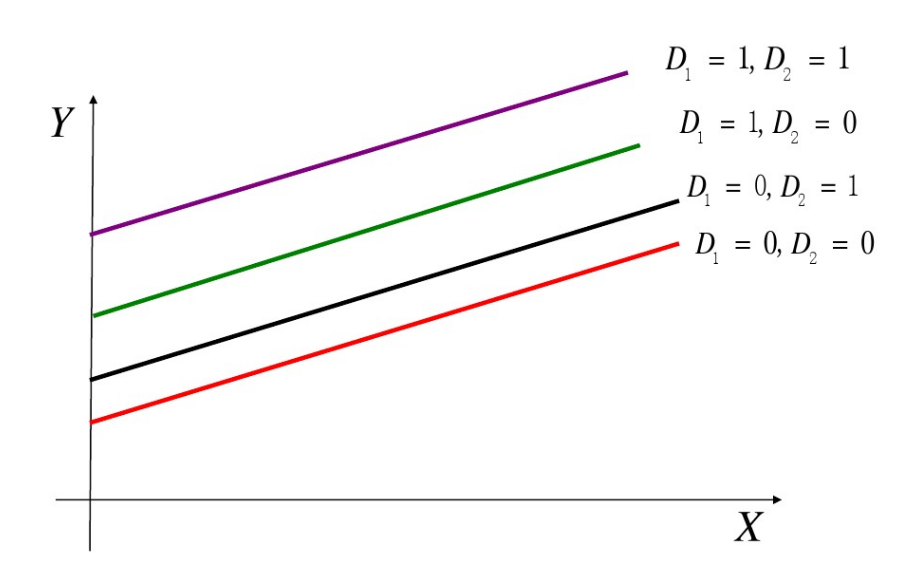
其特点是斜率不变
加法模型的变种
引入交互作用
$Y=a_1+a_2D_1+a_3D_2+a_4D_1D_2+bX+u$
乘法模型
$Y=a_1+a_2D+b_1X+b_2DX+u$
特点是截距斜率都变化
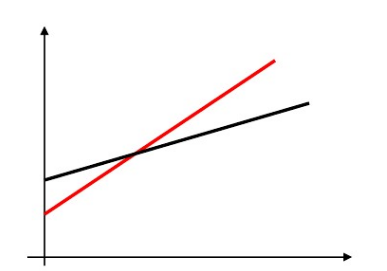
乘法模型的变种
$Y=a_1+b_1X+b_2DX+u$
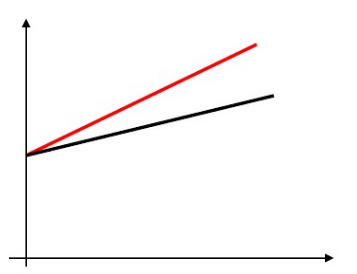
分段模型
$Y=a_0+b_1X+b_2(X-X^* )D+u$
其中,
\(D=\left \{ \begin{array}{ccc}
1&X>=X*\\
0&X<X^*
\end{array}\right.\)
图像是一个折线（两条共点的线段）
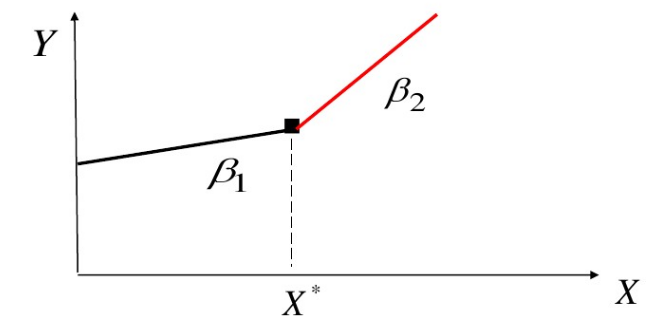
其它虚拟变量回归模型
Dummy Dependent Variables
dependent Variables是dummy，而independent是quantitative Variables。
这实际上是分类模型，有大量的classifier模型可以用，例如决策树模型，SVM等等
用OLS做这个模型，被称为Linear probability model
Linear probability model有诸多缺点，wikipedia总结的很好：
Some problems are inherent in the LPM model:
- The regression line will not be a well-fitted one and hence measures of significance, such as R2, will not be reliable.
- Models that are analyzed using the LPM approach will have heteroscedastic disturbances.
- The error term will have a non-normal distribution.
- The LPM may give predicted values of the dependent variable that are greater than 1 or less than 0. This will be difficult to interpret as the predicted values are intended to be probabilities, which must lie between 0 and 1.
- There might exist a non-linear relationship between the variables of the LPM model, in which case, the linear regression will not fit the data accurately.
为了规避这些缺点，改进为logit regression,见于我的另一篇文章逻辑回归
大名鼎鼎的logit regression本质上可以归类为Dummy Variable Regression
模型检验
- 对整个模型的检验（F检验） H0:$b_1=b_2=…=0$
- 对系数的检验（t检验） H0:$b_j=0$
